算法简介
KMP 算法(Knuth-Morris-Pratt 算法)是一个著名的字符串匹配算法,这个算法由Donald Knuth、Vaughan Pratt、James H. Morris三人于1977年联合发表,故取这3人的姓氏命名此算法。
该算法的执行时间是线性的,且只需要对目标字符串进行预处理,而非搜索的字符串;此算法利用这一特性以避免重新检查先前配对的字符。
该算法通常与BM算法同时被人们提及和熟知,其时间复杂度与空间复杂度均相同,但多数情况下KPM算法实际速度略逊一筹,如果还不了解BM算法,可以参考我的这篇文章:BM字符串匹配算法 | Tony (tonylsx.top)
KMP算法原理
从起始位置不回溯地匹配字符串,当出现失配情况时,利用已经得到的部分结果,尽可能地向右移动更远的位置。具体通过一个next[]数组确定移动多远的距离。
KMP的实现
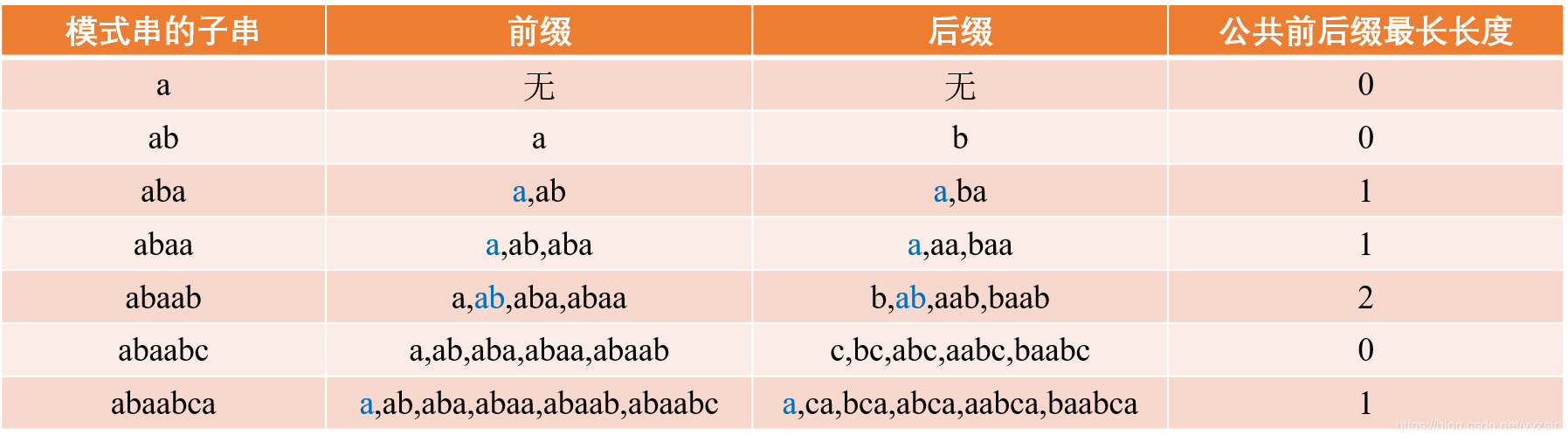
最核心的问题便是如何求解next[]数组。而next[]数组的值即为公共前缀后缀长度向右移动一位的结果,特别的next[0]=-1。
如下面这个例子:string substr="abaabca",他的公共前缀后缀长度为string public="0011201",那么next数组为{-1,0,0,1,1,2,0}.
完整代码
#include <iostream>
#include <string>
#include <vector>
using namespace std;
int KMP(string str, string substr);
int main()
{
string str="abcdfffaerssssse";
string substr="aers";
cout << KMP(str, substr) << endl;
return 0;
}
int KMP(string str, string substr)
{
int n = str.size();
int m = substr.size();
vector<int> next(m);
for (int i = 1, j = 0; i < m; i++)//预处理
{
while (j > 0 && substr[i] != substr[j])
j = next[j - 1];
if (substr[i] == substr[j])
j++;
next[i] = j;
}
for (int i = 0, j = 0; i < n; i++)
{
while (j > 0 && str[i] != substr[j])
j = next[j - 1];
if (str[i] == substr[j])
j++;
if (j == m)
return i - m + 1;
}
}KMP与有限状态自动机
next[]数组可以以有限状态自动机的方式来理解,状态转移图便是next[]数组所储存的信息,一个是当前匹配的状态,另一个是遇到的字符。
如string substr="ABABC",那么他的状态转移图如下所示:
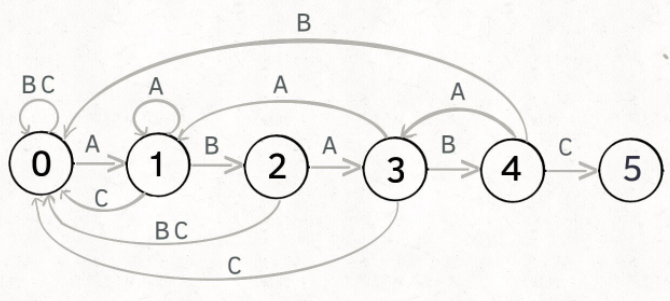
而next[]={-1,0,0,1,1},不知是否看出某些规律呢?
完整代码
#include <iostream>
#include <string>
using namespace std;
const int len=10000;
int dp[len][256];
string str,substr;
void KMP(string pat)
{
int M = pat.length();
// dp[状态][字符] = 下个状态
dp[0][pat[0]] = 1;// base case
int X = 0;// 影子状态 X 初始为 0
for (int j = 1; j < M; j++)// 构建状态转移图
{
for (int c = 0; c < 256; c++)
dp[j][c] = dp[X][c];
dp[j][pat[j]] = j + 1;
X = dp[X][pat[j]];// 更新影子状态
}
}
int search(string txt)
{
int M = substr.length();
int N = txt.length();
int j = 0;// pat 的初始态为 0
for (int i = 0; i < N; i++)
{
j = dp[j][txt[i]];// 计算 pat 的下一个状态
if (j == M) // 到达终止态,返回结果
return i - M + 1;
}
return -1;// 没到达终止态,匹配失败
}
int main()
{
str="aaac5a9aab";
substr="aaab";
KMP(substr);
int ans=search(str);
cout<<ans<<endl;
return 0;
}

