链式二叉树简介

前言

人为什么难做选择？

选择意味着放弃

你选择一方，也就意味着放弃了另一方。摆在你面前的选择项越接近，你的选择就会越困难，因为放弃其中任何一个选择项都不容易。如果摆在你面前的选择项对比明显，那么选择起来就会轻松许多，大家几乎都会毫不犹豫的选择“好”的选择项，放弃掉“差”的选择项。

选择永远都不是完美的

选择永远都不可能十全十美，只可能满足尽量多的侧重点。选择的时候想满足越多的侧重点，可能就会越难做出选择。所以在选择上不要过于追求完美。

警惕逃避性选择——不知道自己要去哪儿，还要选择离开。

有一种选择是对现状不满，想逃离这种现状，但是却不知道去哪里。举个例子，可能目前的公司有各种问题，比如开发流程不规范等，如果因为这些问题离开，可能就会从一个坑跳到另外一个更大的坑。当决定离开的时候，一定是自己有明确的目标，很清楚自己想要什么。

二叉树的定义

二叉树要么为空，要么由根节点（root），左子树（left subtree）和右子树（right subtree）组成，而且左子树和右子树分别是一棵二叉树。说白了就是，二叉树的任何一个节点，有且只能有0，1，2棵子树。

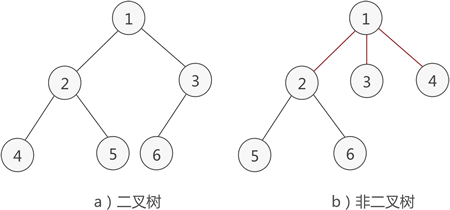
二叉树示意图

二叉树的实现

二叉树的实现方式大致分两种，一种是以数组形式储存，另一种是以链表形式储存。以数组形式储存的好处是实现起来极其便捷，但是数组只能储存完全二叉树，就是二叉树的任何一个父节点（除了叶子节点）都要有两颗子树，如图所示：

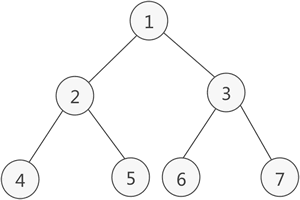
满二叉树示意图

我们这里使用链表的方法维护一个二叉树，一个是这样能够实现更宽泛的二叉树形式，减少内存开销；另外以链表形式实现二叉树可以让我们更加深入理解二叉树的本质。

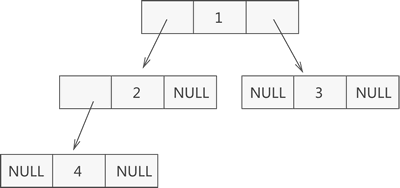
二叉树链式存储结构示意图

头文件

#pragma once
#ifndef BST_H
#define BST_H

struct TreeNode
{
	ElementType Node;
	TreeNode* L_Child;
	TreeNode* R_Child;
};
typedef int ElementType;
typedef struct TreeNode* PtrToNode;
typedef struct TreeNode* Position;
typedef struct TreeNode* SearchTree;

SearchTree MakeEmpty(SearchTree T);//initialize
Position Find(ElementType X, SearchTree T);
Position FindMin(SearchTree T);
Position FindMax(SearchTree T);
SearchTree Insert(SearchTree T, ElementType X);
SearchTree Delete(SearchTree T, ElementType X);
ElementType Retrieve(Position P);//Output

void PreOrderTraverse(SearchTree T);
void InOrderTraverse(SearchTree T);
void PostOrderTraverse(SearchTree T);

#endif

创建二叉树

SearchTree MakeEmpty(SearchTree T)
{
	if (T != NULL)
	{
		MakeEmpty(T->L_Child);
		MakeEmpty(T->R_Child);
		free(T);
	}
	return NULL;
}

二叉树查找元素

Position Find(ElementType X, SearchTree T)
{
	if(T == NULL)
		return NULL;
	if (X < T->Node)
		Find(X, T->L_Child);
	else if (X > T->Node)
		Find(X, T->R_Child);
	else
		return T;
}

查找最大最小值

Position FindMin(SearchTree T)//递归写法
{
	if (T == NULL)
		return NULL;
	else if (T->L_Child == NULL)
		return T;
	else
		return FindMin(T->L_Child);
}
Position FindMax(SearchTree T)//while循环写法
{
	if (T == NULL)
		return NULL;
	else
	{
		while(T->R_Child != NULL)
			T=T->R_Child;
		return T;
	}
}

二叉树插入元素

SearchTree Insert(SearchTree T, ElementType X)
{
	if (T==NULL)// the fist element
	{
		T = new TreeNode;
		T->L_Child = NULL;
		T->R_Child = NULL;
		T->Node = X;
	}
	else
	{
		if (X < T->Node)//put X on the left
			T->L_Child=Insert(T->L_Child, X);
		else             //put X on the right
			T->R_Child = Insert(T->R_Child, X);
	}
	return T;
}

二叉树删除元素

SearchTree Delete(SearchTree T, ElementType X)
{
	if (T == NULL)
		return NULL;
	if (X < T->Node)
	{
		T->L_Child= Delete(T->L_Child, X);
	}
	else if (X > T->Node)
	{
		T->R_Child=Delete(T->R_Child, X);
	}
	else
	{
		if (T->L_Child && T->R_Child) // 2  children
		{
			Position minn = FindMin(T->R_Child);
			T->Node = minn->Node;
			T->R_Child = Delete(T->R_Child, T->Node);

		}
		else           // 1  or  0 child
		{
			Position temp = T;
			if (T->L_Child == NULL)
				T = T->R_Child;
			else if (T->R_Child == NULL)
				T = T->L_Child;
			free(temp);
		}
	}
	return T;
}

二叉树的遍历

先序遍历 $PreOrder(T)=Root(T)+PreOrder(left subT)+PreOrder(right subT)$
中序遍历 $InOrder(T)=InOrder(left subT)+Root(T)+InOrder(right subT)$
后序遍历 $PostOrder(T)=PostOrder(left subT)+PostOrder(Right subT)+Root(T)$

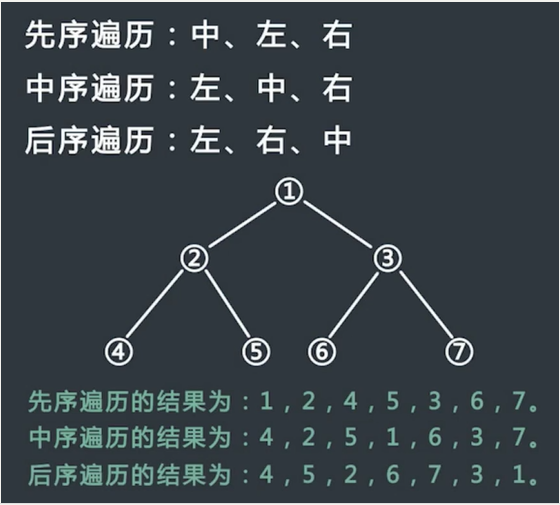
先序遍历

递归实现

void PreOrderTraverse(SearchTree T)
{
	if (T == NULL)
		return;
	cout << Retrieve(T)<<" ";
	PreOrderTraverse(T->L_Child);
	PreOrderTraverse(T->R_Child);
}

迭代实现

void PreOrder(BiTree Root)
{
    stack <BiTree> s;
    if (root) //如果根节点不为空
        s.push(root); //则令根节点入栈
    while (!s.empty()) //在栈变空之前反复循环
    { 
        root = s.pop(); 
        cout << root->data; //弹出并访问当前节点
        //下面左右孩子的顺序不能颠倒
        //必须先让右孩子先入栈，再让左孩子入栈。
        if (root->RChild)
            s.push(root->RChild); //右孩子先入后出
        if (root->LChild)
            s.push(root->LChild); //左孩子后入先出
    }
}

我们通过一个实例来了解一下该迭代版本是如何工作的 :

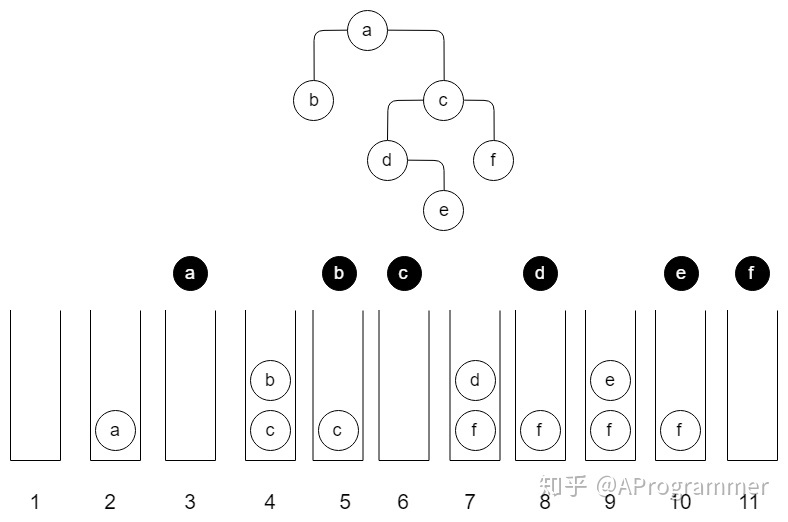
中序遍历

递归实现

void InOrderTraverse(SearchTree T)
{
	if (T == NULL)
		return;
	InOrderTraverse(T->L_Child);
	cout << Retrieve(T) << " ";
	InOrderTraverse(T->R_Child);
}

迭代实现

void InOrderTraverse(BiTree root)
{
   Stack<BiTree> S; //辅助栈
   while (true)
      if (root) 
      {
         S.push (root); //根节点进栈
         root = root->LChild; //深入遍历左子树
      } 
      else if (!S.empty()) 
      {
         root = S.pop(); //尚未访问的最低祖先节点退栈
         cout << root->data; //访问该祖先节点
         root = root->RChild; //遍历祖先的右子树
      } 
      else
         break; //遍历完成
}

后序遍历

递归实现

void PostOrderTraverse(SearchTree T)
{
	if (T == NULL)
		return;
	PostOrderTraverse(T->L_Child);
	PostOrderTraverse(T->R_Child);
	cout << T->Node << " ";
}

迭代实现

#define A !cur->Lchild && !cur->Rchild
//如果P不存在左孩子和右孩子，则可以直接访问它；
#define B pre==cur->Lchild || pre==cur->Rchild
//P存在左孩子或者右孩子，但是其左孩子和右孩子都已被访问过了;
void PostOrder(BiTree Root)
{
    if (!Root)
        return;
    stack <BiTree> s;//辅助栈
    BiTree cur=Root,pre=NULL;
    s.push(Root);//根节点进栈
    while (!s.empty())
    {
        cur=s.top();
        if (A || B)
        {
            cout << cur->data;
            s.pop();
            pre=cur;
        }
        else
        {
            if (cur->Rchild)
                s.push(cur->Rchild);
            if (cur->Lchild)
                s.push(cur->Lchild);
        }
    }
}

main()函数

int main()
{
	SearchTree My_Tree = NULL;
	My_Tree = MakeEmpty(My_Tree);
	My_Tree = Insert(My_Tree, 3);
	My_Tree = Insert(My_Tree, 2);
	My_Tree = Insert(My_Tree, 6);
	My_Tree = Insert(My_Tree, 5);
	My_Tree = Insert(My_Tree, 4);
	if (!Find(1, My_Tree))
		My_Tree = Insert(My_Tree, 1);
	My_Tree = Delete(My_Tree, 1);
	SearchTree min = FindMin(My_Tree);
	cout << Retrieve(min) << endl;
	PreOrderTraverse(My_Tree);
	InOrderTraverse(My_Tree);
	PostOrderTraverse(My_Tree);
	return 0;
}

下一篇文章：数组与链式二叉树之间的转换 | Tony (tonylsx611.github.io)

注：本文图片部分选自http://data.biancheng.net/；如有侵权，请联系我。