二叉树进阶与习题

前言

对二叉树不是很了解的同学可以先看一下我之前的文章：链式二叉树简介

数组二叉树转链表

将一棵完全二叉树转换成链表形式是比较常见的一种做法，我们首先声明一个int类型的数组，然后把它放入链表二叉树中。这个过程相对来说是很容易实现的。

int length = 7;
int arr[length] = { 1, 2, 3, 4, 5, NULL, 6 };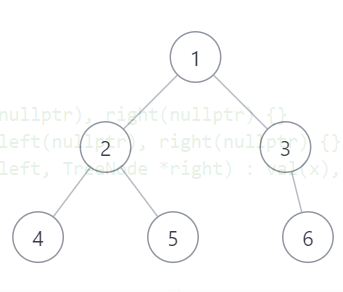

之后的任务就是将数组转化为链表形式，链表的定义如下：

struct TreeNode //二叉树的格式
{
    int val;
    TreeNode* left;
    TreeNode* right;
    TreeNode() : val(0), left(nullptr), right(nullptr) {}
    TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
    TreeNode(int x, TreeNode* left, TreeNode* right) : val(x), left(left), right(right) {}
};

转化的过程也很容易，其实这是一个数学问题，对于一棵完全二叉树（满二叉树），节点tree[i]的左子树永远是tree[2*i+1]，节点tree[i]的右子树永远是tree[2*i+2]；并且我们只需要递归到倒数第二层的树即可，即if (i < length/2)。

TreeNode* addtree(TreeNode* tree, int arr[], int i)//数组转链表
{
	if (arr[i] == 0)
        return NULL;
    if (i < length/2)//arr.length()
    {
        TreeNode* tree = new TreeNode();
        
        tree->val = arr[i];
        tree->left = addtree(tree, arr, i + i + 1);
        tree->right = addtree(tree, arr, i + i + 2);
        return tree;
    }
    return NULL;
}

链表二叉树转数组

比较困难的是如何将链表二叉树转换为数组，因为链表形式下并不一定每一个节点都有两个子节点，因此链表二叉树是没有办法直接转化成一棵数组型的完全二叉树（可能也可以，但是我不会，欢迎在评论区讨论）。

如果可以获得链式二叉树的高度，那么可以通过BFS来遍历整个链表，即使链表的节点没有左枝或右枝，也把一个空节点加进stack中，这样理论上可以实现链表到数组的转换，不过实现起来还是非常麻烦。

因此，我们绝大多数情况下是不会将链表转化成数组的，因为在链表中操作数据是非常方便的（当然在数组中操作也不麻烦），我们做的最多的事情就是搜索和遍历二叉树，如果不是很理解前一句话，建议再次回顾一下上一篇文章：链式二叉树简介

例题98

题目描述

Leetcode链接: 98. 验证二叉搜索树 - 力扣（LeetCode） (leetcode-cn.com)

给你一个二叉树的根节点 root ，判断其是否是一个有效的二叉搜索树。

有效 二叉搜索树定义如下：

• 节点的左子树只包含 小于 当前节点的数。
• 节点的右子树只包含 大于 当前节点的数。
• 所有左子树和右子树自身必须也是二叉搜索树。

输入输出样例：

input: root=[2,1,3]
output: true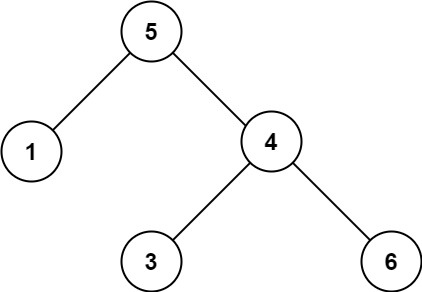

input: root = [5,1,4,null,null,3,6]
output: false
explanation: 根节点的值是 5 ，但是右子节点的值是 4 。

提示：

• 树中节点数目范围在$[1, 10^4]$ 内
• $-2^{31} \leq Node.val \leq 2^{31} - 1$

例题分析

我最初的思路是，只要保证每一个节点大于左枝，小于右枝即可。

对于这样的思路，直接对链表进行BFS搜索即可，如果不会BFS算法，可以参考：BFS简介。当然，其他的搜索算法也可以考虑，比如DFS，或者前序中序后序遍历每一个节点，然后判断每个节点的两个子节点就可以。我这里就用BFS来实现，代码如下：

class Solution {
public:
    TreeNode* temp;
    bool isValidBST(TreeNode* root)
    {
        queue<TreeNode*> Q;
        TreeNode* node;
        Q.push(root);
        while (!Q.empty())
        {
            node = Q.front();
            temp = node;
            if (node->left != NULL)
            {
                if (node->left->val >= temp->val)
                    return false;
                Q.push(node->left);
            }
            if (node->right != NULL)
            {
                if (node->right->val <= temp->val)
                    return false;
                Q.push(node->right);
            }
            Q.pop();
        }
        return true;
    }
};

但是，我发现我的理解是有问题的，这个题目要求是节点下面的所有左子树的值都要小于该节点，节点下面所有右子树的值都要大于该节点！

比如这个例子，对于该题来说，他的答案应该是false。因为根节点的值是5，但是右侧分支中有一个节点的值是3，小于根节点的值。

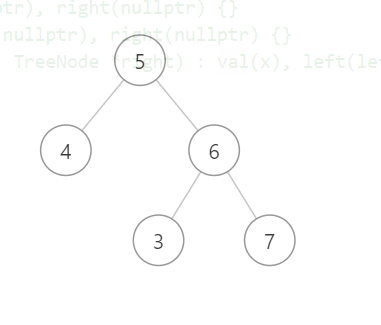
因此，对于这种情况，我们应该优先考虑对二叉树进行中序遍历，中序遍历的结果如果是升序就返回true，否则返回false。

比如上面这个错误的样例的中序遍历结果为：root=[4,5,3,6,7];，他不是单调递增的数组。

再比如，我们来看一个正确的样例，他的中序遍历的结果为：root=[4,5,6,7,9]，他是单调递增的数组。

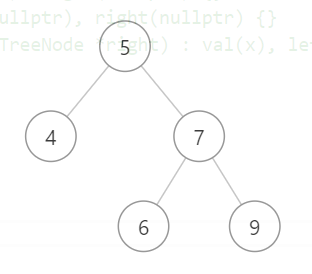
因此，我们的思路就可以转变为，判断该二叉树的中序遍历结果是否为单调递增，来判断其是否是一个有效的二叉搜索树，代码如下：

class Solution {
public:
    int btree[10001];
    int ptr = 0;
    void inorder(TreeNode* root)
    {
        if (root == NULL)
            return;
        if (root->left)
            inorder(root->left);
        btree[ptr] = root->val;
        ptr++;
        if (root->right)
            inorder(root->right);
    }
    bool isValidBST(TreeNode* root)
    {
        inorder(root);
        //for(int i=0;i<ptr;i++)
        //    cout<<btree[i]<<" ";    
        for (int i = 0; i < ptr - 1; i++)
            if (btree[i] >= btree[i + 1])
                return false;
        return true;
    }
};

例题103

题目描述

Leetcode链接: 103. 二叉树的锯齿形层序遍历 - 力扣（LeetCode） (leetcode-cn.com)

给你二叉树的根节点 root ，返回其节点值的 锯齿形层序遍历 。（即先从左往右，再从右往左进行下一层遍历，以此类推，层与层之间交替进行）。

输入输出样例：

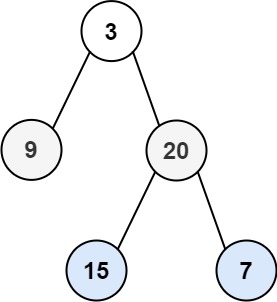
输入：root = [3,9,20,null,null,15,7]
输出：[[3],[20,9],[15,7]]

输入：root = [1]
输出：[[1]]

输入：root = []
输出：[]

提示：

• 树中节点数目在范围 $[0, 2000]$ 内
• $-100 \leq Node.val \leq 100$

题目分析

官方的题解以及很多人都很喜欢使用deque(双端队列)来做，这种做法自然很好，但是我们明明用正常的队列就可以搞定的事，干嘛那么复杂呢？

首先分析题目，既然要求一层层地遍历二叉树，那么自然而然就应该想到用BFS来遍历。然而正常的BFS是没办法分层的，就是说我们BFS仅仅是维护了一个栈，但实际上无法将层与层之间的节点分离开来。我们只需要稍作改动，在while循环中嵌套一个for循环即可实现。想一想为什么？

回忆一下BFS的原理，每次进栈的节点深度都一样，每次出栈的节点深度也是一样的，利用这个原理，就可以将每一层的节点分开，输出到二维vector数组中。

至于还要从右向左遍历，我们只需要构建一个reverse函数，将二维数组双数的行不变，单数的行取反reverse，就好啦。

需要注意的是，我们应该了解如何使用vector创建二维数组，每次for循环都用resize创建一行vector数组。如果不熟悉的话建议百度一下。。。（比如说我就不太会）

全部代码如下，建议去leetcode自行做一下，不要抄任何现成的代码，这样对能力提升没好处。

class Solution {
public:
    vector<vector<int>> zigzagLevelOrder(TreeNode* root) 
    {
        vector<vector<int>> ans;
        queue<TreeNode*> Q;
        if(root)
            Q.push(root);
        else
            return ans;
        int depth=0;
        while(!Q.empty())
        {
            ans.resize(depth+1); 
            int temp=Q.size();
            for(int i=0;i<temp;i++)//循环每一层
            {
                TreeNode* node;
                node=Q.front();
                if(node->left != NULL)
                    Q.push(node->left);
                if(node->right != NULL)
                    Q.push(node->right);
                ans[depth].push_back(node->val);
                Q.pop();
            }
            depth++;
        }
        for(int i=1;i<depth;i+=2)
            reverse(ans[i]);
        return ans;
    }
    vector<int> reverse(vector<int>& arr)
    {
        int len=arr.size();
        if(len<=1)
            return arr;
        for(int i=0;i<len/2;i++)//reverse
        {
            int temp=arr[i];
            arr[i]=arr[len-i-1];
            arr[len-i-1]=temp;
        }
        return arr;
    }
};